2023-05-07 23:34:30
– Stop the search! We’ve found it at last,’ exclaimed Commissioner MacCarnigan.
– Who sir? asked Second Lieutenant Pierron.
– To one of the most slippery rogues you could ever imagine. I’ve been looking for it for almost 50 years.
– I had no idea, sir. Who is it about?
– His name is Ein Stein and it has taken me almost a lifetime to find him.
– Who is it about? Do you have any photos of yourself out there?
– Yes, I have it right here, this is what it looks like, but don’t be fooled by its innocent appearance, this gentleman here has kept us in suspense for almost ten decades.
So MacCarnigan showed Agent Pierron the photo of this Ein Stein, this photo:
A rock.
This brief history of policemen may seem like a joke, but if we change detectives for mathematicians, it becomes one of the most wonderful mathematical discoveries that have occurred in recent years. But in order to understand the magnitude of this story, we first have to talk about one of the fields in which mathematics and art merge: mosaics.
periodic tiles
We have all seen a mosaic at some point in our lives. These are small artistic or decorative works that are made using small pieces that fit together.


Some examples of mosaics
When we talk about mosaics in mathematics, we usually refer to what is known as tessellations, which is a way of arranging pieces or tiles so that these pieces have common edges and do not leave holes.
A long time ago, mathematicians and mathematics asked themselves the following question
What kind of pieces can I tile the plane with?
That is, what type of pieces can I use so that, placing them so that the tiles touch each other on common sides, there are no gaps in the plane. Clearly the circles are not in this select group, since if I want to tile the plane using only circles they will leave me with holes. Come on, I’m going to have to put fixed grout.

Circles leave gaps
However, there are many other shapes with which we can tile the plane, such as triangles, squares or hexagons.

Tessellation with a single regular polygon
Or we can tile the plane with combinations of these or other figures.

Tessellation with several regular polygons
Or you can even tile the plane with more extravagant combinations:

Other possible tilings
But despite the great variety of tilings that have been presented, they all have something in common, and that is that they are periodic. The term periodic refers to the fact that there is some translation, other than zero, that leaves the whole mosaic the same. So that we understand each other, this is equivalent to the fact that if we tile a surface, we close our eyes and someone moves the whole mosaic in a certain direction and then we open our eyes again, we will be unable to appreciate the difference between the original mosaic and the displaced one. .
non-periodic tiles
In contrast to periodic tilings we find non-periodic tilings, which are those for which there is no translation, not zero, that leaves the mosaic with the same appearance. It is not difficult to find non-periodic mosaics, it is enough, for example, to take a periodic tiling, let us think, for example, one formed only by squares, and a single square of the entire mosaic is divided into two triangles. Clearly it is still a tessellation of the plane, but there will be no translation that will leave the entire tesserae the same, since we will be able to distinguish between the original mosaic and its displaced one simply by observing the modified position of the two triangles.
aperiodic tiling
But now is when things get interesting, because it is when the concept of aperiodic mosaic appears, which are those that, being non-periodic, satisfy the extra condition that they do not have arbitrarily large regions that are periodic. In the same way, this idea can be understood as that in an aperiodic mosaic, if we take a large enough piece, it is not repeated in the rest of the mosaic. It should be noted that the example of a non-periodic mosaic described above is not aperiodic since we can find arbitrarily large regions that are periodic, it is enough to take arbitrarily large pieces that do not include any of the two triangles.
So, the question that naturally arises is the following:
Are there aperiodic mosaics?
This question, which began to be studied in the second half of the last century, soon received an affirmative answer and one of the first to find an aperiodic tiling was Raphael M. Robinson. The mosaic described by Robinson in 1971 is made up of the following 6 tiles.
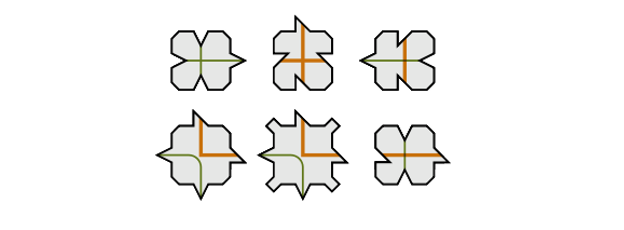
Robinson tiles
A few years later, also in the 1970s, Roger Penrose obtained two aperiodic tessellations that could be built, each using only two different tesserae. The first of these tessellations is formed by two different rhombuses:
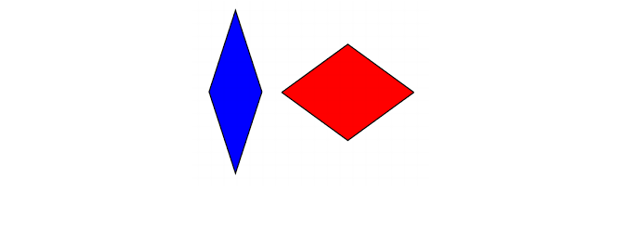
Penrose tiles (rhombuses)
And it is capable of producing mosaics like the following:
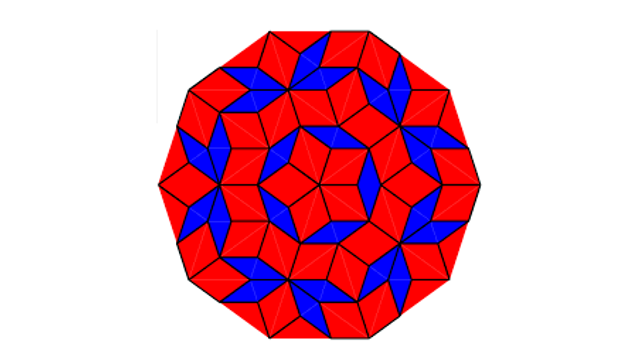
penrose mosaic
The second of these aperiodic tilings is given by two pieces known as kite and arrow, for obvious reasons:
Penrose tiles (comet and arrow)
Well, and now the question that one could ask is the following:
Are there aperiodic mosaics formed by a single tile?
This problem has been known as the Ein Stein problem (German for “a stone”) and for almost 50 years it has remained unsolved. Until last March!
The discovery of the Ein Stein
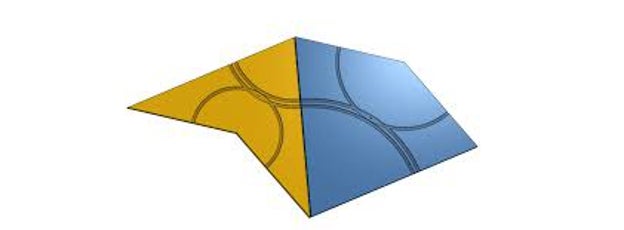
On March 20, scientists David Smith, Joseph Samuel Myers, Craig S. Kaplan y Chaim Goodman-Strauss from the Universities of Cambridge, Waterloo and Arkansas published the work ‘An aperiodic monotile’ in which they describe a possible form of the much sought after tesserae that gives rise to an aperiodic mosaic with a single piece.
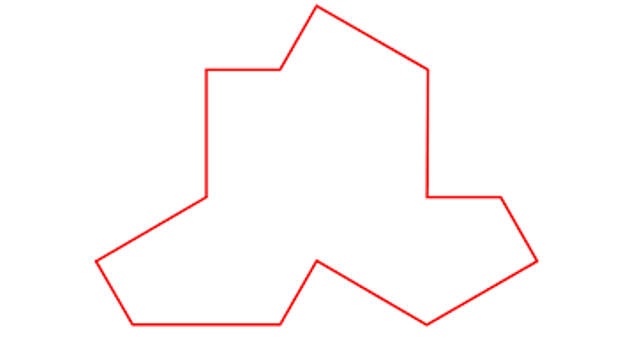
Tile described by Smith, Myers, Kaplan and Goodman-Strauss
With this single tile, which seems to me to be very similar to a T-shirt, they demonstrate that aperiodic mosaics such as the following can be built:

Aperiodic mosaic of a tile
If you are curious about the subject, you can delve deeper into this discovery in the following video,
in which its discoverers speak with other relevant people in the area, including the Nobel Prize in Physics Roger Penrose.
The ABCdario de las Matemáticas is a section that arises from the collaboration with the Dissemination Commission of the Royal Spanish Mathematical Society (RSME).
#Mathematicians #discover #shirt #pattern #repeats

 Victor M. Manero
Victor M. Manero